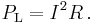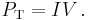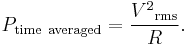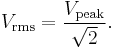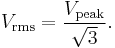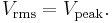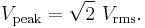Alternating current

In alternating current (AC, also ac) the movement of electric charge periodically reverses direction. In direct current (DC), the flow of electric charge is only in one direction.
AC is the form in which electric power is delivered to businesses and residences. The usual waveform of an AC power circuit is a sine wave. In certain applications, different waveforms are used, such as triangular or square waves. Audio and radio signals carried on electrical wires are also examples of alternating current. In these applications, an important goal is often the recovery of information encoded (or modulated) onto the AC signal.
Contents |
History


(US patent 373035)
The first inventor to use alternating current was apparently Guillaume Duchenne, the developer of electrotherapy. In 1855, he announced that alternating was superior to direct current for electrotherapeutic triggering of muscle contractions.[1]
A power transformer developed by Lucien Gaulard and John Dixon Gibbs was demonstrated in London in 1881, and attracted the interest of Westinghouse. They also exhibited the invention in Turin in 1884, where it was adopted for an electric lighting system. Many of their designs were adapted to the particular laws governing electrical distribution in the UK.
In 1882, 1884, and 1885 Gaulard and Gibbs applied for patents on their transformer; however, these were overturned due to prior arts of Nikola Tesla and actions initiated by Sebastian Ziani de Ferranti.
Ferranti went into this business in 1882 when he set up a shop in London designing various electrical devices. Ferranti believed in the success of alternating current power distribution early on, and was one of the few experts in this system in the UK. In 1887 the London Electric Supply Corporation (LESCo) hired Ferranti for the design of their power station at Deptford. He designed the building, the generating plant and the distribution system. On its completion in 1891 it was the first truly modern power station, supplying high-voltage AC power that was then "stepped down" for consumer use on each street. This basic system remains in use today around the world. Many homes all over the world still have electric meters with the Ferranti AC patent stamped on them.
William Stanley, Jr. designed one of the first practical devices to transfer AC power efficiently between isolated circuits. Using pairs of coils wound on a common iron core, his design, called an induction coil, was an early transformer. The AC power system used today developed rapidly after 1886, and includes key concepts by Nikola Tesla, who subsequently sold his patent to George Westinghouse. Lucien Gaulard, John Dixon Gibbs, Carl Wilhelm Siemens and others contributed subsequently to this field. AC systems overcame the limitations of the direct current system used by Thomas Edison to distribute electricity efficiently over long distances even though Edison attempted to discredit alternating current as too dangerous during the War of Currents.
The first commercial power plant in the United States using three-phase alternating current was at the Mill Creek No. 1 Hydroelectric Plant near Redlands, California, in 1893 designed by Almirian Decker. Decker's design incorporated 10,000-volt three-phase transmission and established the standards for the complete system of generation, transmission and motors used today.
The Ames Hydroelectric Generating Plant (spring of 1891) and the original Niagara Falls Adams Power Plant (August 25, 1895) were among the first AC-powered hydroelectric plants.
The Jaruga Hydroelectric Power Plant in Croatia was set in operation on 28 August 1895. The two generators (42 Hz, 550 kW each) and the transformers were produced and installed by the Hungarian company Ganz. The transmission line from the power plant to the City of Šibenik was 11.5 kilometers (7.1 mi) long on wooden towers, and the municipal distribution grid 3000 V/110 V included six transforming stations.
Alternating current circuit theory developed rapidly in the latter part of the 19th and early 20th century. Notable contributors to the theoretical basis of alternating current calculations include Charles Steinmetz, James Clerk Maxwell, Oliver Heaviside, and many others. Calculations in unbalanced three-phase systems were simplified by the symmetrical components methods discussed by Charles Legeyt Fortescue in 1918.
Transmission, distribution, and domestic power supply
Alternating Current voltage may be increased or decreased with a transformer. Use of a higher voltage leads to significantly more efficient transmission of power. The power losses in a conductor are a product of the square of the current and the resistance of the conductor, described by the formula
This means that when transmitting a fixed power on a given wire, if the current is doubled, the power loss will be four times greater.
The power transmitted is equal to the product of the current and the voltage (assuming no phase difference); that is,
Thus, the same amount of power can be transmitted with a lower current by increasing the voltage. It is therefore advantageous when transmitting large amounts of power to distribute the power with high voltages (often hundreds of kilovolts).

However, high voltages also have disadvantages, the main one being the increased insulation required, and generally increased difficulty in their safe handling. In a power plant, power is generated at a convenient voltage for the design of a generator, and then stepped up to a high voltage for transmission. Near the loads, the transmission voltage is stepped down to the voltages used by equipment. Consumer voltages vary depending on the country and size of load, but generally motors and lighting are built to use up to a few hundred volts between phases.
The utilization voltage delivered to equipment such as lighting and motor loads is standardized, with an allowable range of voltage over which equipment is expected to operate. Standard power utilization voltages and percentage tolerance vary in the different mains power systems found in the world.
Modern high-voltage, direct-current electric power transmission systems contrast with the more common alternating-current systems as a means for the efficient bulk transmission of electrical power over long distances. HVDC systems, however, tend to be more expensive and less efficient over shorter distances than transformers. Transmission with high voltage direct current was not feasible when Edison, Westinghouse and Tesla were designing their power systems, since there was then no way to economically convert AC power to DC and back again at the necessary voltages.
Three-phase electrical generation is very common. Three separate coils in the generator stator are physically offset by an angle of 120° to each other. Three current waveforms are produced that are equal in magnitude and 120° out of phase to each other.
If the load on a three-phase system is balanced equally among the phases, no current flows through the neutral point. Even in the worst-case unbalanced (linear) load, the neutral current will not exceed the highest of the phase currents. Non-linear loads (e.g. computers) may require an oversized neutral bus and neutral conductor in the upstream distribution panel to handle harmonics. Harmonics can cause neutral conductor current levels to exceed that of one or all phase conductors.
For three-phase at utilization voltages a four-wire system is often used. When stepping down three-phase, a transformer with a Delta (3-wire) primary and a Star (4-wire, center-earthed) secondary is often used so there is no need for a neutral on the supply side.
For smaller customers (just how small varies by country and age of the installation) only a single phase and the neutral or two phases and the neutral are taken to the property. For larger installations all three phases and the neutral are taken to the main distribution panel. From the three-phase main panel, both single and three-phase circuits may lead off.
Three-wire single phase systems, with a single center-tapped transformer giving two live conductors, is a common distribution scheme for residential and small commercial buildings in North America. This arrangement is sometimes incorrectly referred to as "two phase". A similar method is used for a different reason on construction sites in the UK. Small power tools and lighting are supposed to be supplied by a local center-tapped transformer with a voltage of 55 V between each power conductor and earth. This significantly reduces the risk of electric shock in the event that one of the live conductors becomes exposed through an equipment fault whilst still allowing a reasonable voltage of 110 V between the two conductors for running the tools.
A third wire, called the bond (or earth) wire, is often connected between non-current-carrying metal enclosures and earth ground. This conductor provides protection from electric shock due to accidental contact of circuit conductors with the metal chassis of portable appliances and tools. Bonding all non-current-carrying metal parts into one complete system ensures there is always a low electrical impedance path to ground sufficient to carry any fault current for as long as it takes for the system to clear the fault. This low impedance path allows the maximum amount of fault current, causing the overcurrent protection device (breakers, fuses) to trip or burn out as quickly as possible, bringing the electrical system to a safe state. All bond wires are bonded to ground at the main service panel, as is the Neutral/Identified conductor if present.
AC power supply frequencies
The frequency of the electrical system varies by country; most electric power is generated at either 50 or 60 Hz. Some countries have a mixture of 50 Hz and 60 Hz supplies, notably Japan.
A low frequency eases the design of low speed electric motors, particularly for hoisting, crushing and rolling applications, and commutator-type traction motors for applications such as railways, but also causes a noticeable flicker in incandescent lighting and an objectionable flicker in fluorescent lamps. 16⅔ Hz power is still used in some European rail systems, such as in Austria, Germany, Norway, Sweden and Switzerland. The use of lower frequencies also provided the advantage of lower impedance losses, which are proportional to frequency. The original Niagara Falls generators were built to produce 25 Hz power, as a compromise between low frequency for traction and heavy induction motors, while still allowing incandescent lighting to operate (although with noticeable flicker); most of the 25 Hz residential and commercial customers for Niagara Falls power were converted to 60 Hz by the late 1950s, although some 25 Hz industrial customers still existed as of the start of the 21st century.
Off-shore, military, textile industry, marine, computer mainframe, aircraft, and spacecraft applications sometimes use 400 Hz, for benefits of reduced weight of apparatus or higher motor speeds.
Effects at high frequencies
A direct current flows constantly and uniformly throughout the cross-section of a uniform wire. An alternating current of any frequency is forced away from the wire's center, toward its outer surface. This is because the acceleration of an electric charge in an alternating current produces waves of electromagnetic radiation that cancel the propagation of electricity toward the center of materials with high conductivity. This phenomenon is called skin effect.
At very high frequencies the current no longer flows in the wire, but effectively flows on the surface of the wire, within a thickness of a few skin depths. The skin depth is the thickness at which the current density is reduced by 63%. Even at relatively low frequencies used for high power transmission (50–60 Hz), non-uniform distribution of current still occurs in sufficiently thick conductors. For example, the skin depth of a copper conductor is approximately 8.57 mm at 60 Hz, so high current conductors are usually hollow to reduce their mass and cost.
Since the current tends to flow in the periphery of conductors, the effective cross-section of the conductor is reduced. This increases the effective AC resistance of the conductor, since resistance is inversely proportional to the cross-sectional area in which the current actually flows. The AC resistance often is many times higher than the DC resistance, causing a much higher energy loss due to ohmic heating (also called I2R loss).
Techniques for reducing AC resistance
For low to medium frequencies, conductors can be divided into stranded wires, each insulated from one other, and the relative positions of individual strands specially arranged within the conductor bundle. Wire constructed using this technique is called Litz wire. This measure helps to partially mitigate skin effect by forcing more equal current throughout the total cross section of the stranded conductors. Litz wire is used for making high-Q inductors, reducing losses in flexible conductors carrying very high currents at lower frequencies, and in the windings of devices carrying higher radio frequency current (up to hundreds of kilohertz), such as switch-mode power supplies and radio frequency transformers.
Techniques for reducing radiation loss
As written above, an alternating current is made of electric charge under periodic acceleration, which causes radiation of electromagnetic waves. Energy that is radiated is lost. Depending on the frequency, different techniques are used to minimize the loss due to radiation.
Twisted pairs
At frequencies up to about 1 GHz, pairs of wires are twisted together in a cable, forming a twisted pair. This reduces losses from electromagnetic radiation and inductive coupling. A twisted pair must be used with a balanced signalling system, so that the two wires carry equal but opposite currents. Each wire in a twisted pair radiates a signal, but it is effectively cancelled by radiation from the other wire, resulting in almost no radiation loss.
Coaxial cables
Coaxial cables are commonly used at audio frequencies and above for convenience. A coaxial cable has a conductive wire inside a conductive tube, separated by a dielectric layer. The current flowing on the inner conductor is equal and opposite to the current flowing on the inner surface of the tube. The electromagnetic field is thus completely contained within the tube, and (ideally) no energy is lost to radiation or coupling outside the tube. Coaxial cables have acceptably small losses for frequencies up to about 5 GHz. For microwave frequencies greater than 5 GHz, the losses (due mainly to the electrical resistance of the central conductor) become too large, making waveguides a more efficient medium for transmitting energy. Coaxial cables with an air rather than solid dielectric are preferred as they transmit power with lower losses.
Waveguides
Waveguides are similar to coax cables, as both consist of tubes, with the biggest difference being that the waveguide has no inner conductor. Waveguides can have any arbitrary cross section, but rectangular cross sections are the most common. Because waveguides do not have an inner conductor to carry a return current, waveguides cannot deliver energy by means of an electric current, but rather by means of a guided electromagnetic field. Although surface currents do flow on the inner walls of the waveguides, those surface currents do not carry power. Power is carried by the guided electromagnetic fields. The surface currents are set up by the guided electromagnetic fields and have the effect of keeping the fields inside the waveguide and preventing leakage of the fields to the space outside the waveguide.
Waveguides have dimensions comparable to the wavelength of the alternating current to be transmitted, so they are only feasible at microwave frequencies. In addition to this mechanical feasibility, electrical resistance of the non-ideal metals forming the walls of the waveguide cause dissipation of power (surface currents flowing on lossy conductors dissipate power). At higher frequencies, the power lost to this dissipation becomes unacceptably large.
Fiber optics
At frequencies greater than 200 GHz, waveguide dimensions become impractically small, and the ohmic losses in the waveguide walls become large. Instead, fiber optics, which are a form of dielectric waveguides, can be used. For such frequencies, the concepts of voltages and currents are no longer used.
Mathematics of AC voltages

Alternating currents are accompanied (or caused) by alternating voltages. An AC voltage v can be described mathematically as a function of time by the following equation:
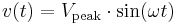 ,
,
where
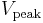 is the peak voltage (unit: volt),
is the peak voltage (unit: volt),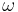 is the angular frequency (unit: radians per second)
is the angular frequency (unit: radians per second)
- The angular frequency is related to the physical frequency,
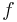 (unit = hertz), which represents the number of cycles per second , by the equation
(unit = hertz), which represents the number of cycles per second , by the equation 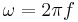 .
.
- The angular frequency is related to the physical frequency,
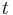 is the time (unit: second).
is the time (unit: second).
The peak-to-peak value of an AC voltage is defined as the difference between its positive peak and its negative peak. Since the maximum value of 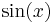 is +1 and the minimum value is −1, an AC voltage swings between
is +1 and the minimum value is −1, an AC voltage swings between 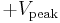 and
and 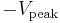 . The peak-to-peak voltage, usually written as
. The peak-to-peak voltage, usually written as 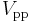 or
or 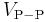 , is therefore
, is therefore 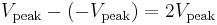 .
.
Power and root mean square
The relationship between voltage and the power delivered is
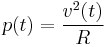 where
where  represents a load resistance.
represents a load resistance.
Rather than using instantaneous power, 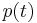 , it is more practical to use a time averaged power (where the averaging is performed over any integer number of cycles). Therefore, AC voltage is often expressed as a root mean square (RMS) value, written as
, it is more practical to use a time averaged power (where the averaging is performed over any integer number of cycles). Therefore, AC voltage is often expressed as a root mean square (RMS) value, written as 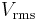 , because
, because
For a sinusoidal voltage:
The factor  is called the crest factor, which varies for different waveforms.
is called the crest factor, which varies for different waveforms.
- For a triangle wave form centered about zero
- For a square wave form centered about zero
Example
To illustrate these concepts, consider a 230 V AC mains supply used in many countries around the world. It is so called because its root mean square value is 230 V. This means that the time-averaged power delivered is equivalent to the power delivered by a DC voltage of 230 V. To determine the peak voltage (amplitude), we can rearrange the above equation to:
For our 230 V AC, the peak voltage Vpeak is therefore 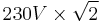 , which is about 325 V. The peak-to-peak value
, which is about 325 V. The peak-to-peak value 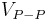 of the 230 V AC is double that, at about 650 V.
of the 230 V AC is double that, at about 650 V.
Note that some countries use a frequency of 50 Hz, while others use a frequency of 60 Hz. The calculation to convert from RMS voltage to peak voltage is independent of the frequency.
See also
- AC power
- Direct current
- Electrical wiring
- Heavy-duty power plugs
- Hertz
- Mains power systems
- AC power plugs and sockets
- Utility frequency
- War of Currents
Further reading
- Willam A. Meyers, History and Reflections on the Way Things Were: Mill Creek Power Plant - Making History with AC, IEEE Power Engineering Review, February 1997, Pages 22–24
External links
- "Alternating Current: Alternating Current". Interactive Java tutorial explaining alternating current. (National High Magnetic Field Laboratory)
- "AC/DC: What's the Difference?". Edison's Miracle of Light, American Experience. (PBS)
- "AC/DC: Inside the AC Generator". Edison's Miracle of Light, American Experience. (PBS)
- Kuphaldt, Tony R., "Lessons In Electric Circuits : Volume II - AC". March 8, 2003. (Design Science License)
- Nave, C. R., "Alternating Current Circuits Concepts". HyperPhysics.
- "Alternating Current (AC)". Magnetic Particle Inspection, Nondestructive Testing Encyclopedia.
- "Alternating current". Analog Process Control Services.
- Hiob, Eric, "An Application of Trigonometry and Vectors to Alternating Current". British Columbia Institute of Technology, 2004.
- "Introduction to alternating current and transformers". Integrated Publishing.
- "Wind Energy Reference Manual Part 4: Electricity". Danish Wind Industry Association, 2003.
- Chan. Keelin, "Alternating current Tools". JC Physics, 2002.
- Williams, Trip "Kingpin", "Understanding Alternating Current, Some more power concepts".
- "Table of Voltage, Frequency, TV Broadcasting system, Radio Broadcasting, by Country".
- Professor Mark Csele's tour of the 25 Hz Rankine generating station
- 50/60 hertz information
- AC circuits Animations and explanations of vector (phasor) representation of RLC circuits
- Blalock, Thomas J., "The Frequency Changer Era: Interconnecting Systems of Varying Cycles". The history of various frequencies and interconversion schemes in the US at the beginning of the 20th century
- (Italian) Generating an a.c voltage.Interactive.
- ↑ Licht, Sidney Herman., "History of Electrotherapy", in Therapeutic Electricity and Ultraviolet Radiation, 2nd ed., ed. Sidney Licht, New Haven: E. Licht, 1967, Pp. 1-70.